INTRODUCTION
EXPERIMENTAL TECHNIQUES
Techniques
Uncertainties
Materials
RESULTS
Measurements Across The Frequency Range
Comparison Between Species
LITERATURE SURVEY
Review of the Dielectric Properties of Tissues
Presentation of Data
DATA ANALYSIS
Parametric Description of the Dielectric Spectrum
THE DIELECTRIC PROPERTIES BELOW 100 Hz
Electrical properties of Body Tissues
Electrical properties of Body Parts
CONCLUSIONS
REFERENCES
APPENDIX A: Experimental data.
APPENDIX B1: Literature Survey. (Graphs)
APPENDIX B2: Literature Survey. (Data)
APPENDIX C: Modelling the frequency dependence of the dielectric properties to a 4 dispersions spectrum.
APPENDIX D: Tabulation of the experimental data referred to in Appendix C.
Figure 1. Uncorrected values of the permittivity and conductivity of a series of salt solutions.
Figure 2. Comparison between the dielectric properties of tongue muscle from animal and human samples.
Figure 3. Comparison between the dielectric properties of tendon from two anima species.
Figure 4. Comparison between the dielectric properties of small intestine tissue from animal and human samples.
Table 1. Estimates of the conductivity (S/m) of body tissues below 100 Hz at body temperature.
Table 2. Conductivity, in S/m, of the whole and parts of the body obtained by integrating the conductivity values in Table 1 over various parts of the body.
Recent developments in the field of electromagnetic dosimetry have produced high resolution anatomically correct man and animal models from medical imaging data for use in numerical simulation exercises. The level of details is such that over 30 tissue types can be identified. The application of such models require that dielectric properties be allocated to the various tissues at all the frequencies to which the model is exposed. There is, as yet, no consensus on the dielectric data. This project is geared towards this objective. The following has been achieved in the period covered by this report:
The work is briefly described in this report, the data are presented in graphical and tabular format in Appendices A to D.
The dielectric measurements were performed using automatic swept frequency
network and impedance analysers. For the frequency range 10 Hz to 10 MHz,
an HP4192A impedance analyser. An HP 8753C covered the frequency range
300 kHz to 3 GHz and an HP8720 measured from 130 MHz to 20 GHz. Open ended
coaxial probes were used to interface the measuring equipment with the
samples in all cases. The technique used with the HP8700 series network
analysers has been reported in details elsewhere (Gabriel et al 1994) and
will not be discussed further. The techniques used in conjunction with
the impedance analyser will be briefly described. A 50 ohms impedance matched
conical coaxial probe was adapted (Gabriel and Grant 1988) to interface
the sample to the HP4192A impedance analyser. The probe is characterised
by a fringing capacitance C and conductance G which are a function of its
physical dimension and can be measured with the impedance analyser. The
characteristic parameters of the probe were calculated from measurements
of the impedance components of the probe in air and in a standard sample
(water or salt solution). In principle, the dielectric properties (permittivity
and
conductivity
)
of an unknown sample can then be calculated from measurements of the impedance
of the probe against an unknown sample using the following relationships
where
is
the permittivity of free space
(1)
In practice, the measurement of conductive materials in the frequency
range 10 Hz to 10 MHz are not so straightforward. The measurements are
affected by two sources of systematic errors, electrode polarisation and
lead inductance errors, which become apparent at the lower and higher ends
of the frequency range under consideration. Electrode polarisation is a
manifestation of molecular charge organisation which occur at the sample-electrode
interface in presence of water molecules and hydrated ions. In its simplest
forms the phenomenon is equivalent to a frequency dependent capacitor in
series with a resistor. Both components can be approximated by negative
power functions of frequency, that is their absolute values decrease with
increasing frequency. The effect increases with increasing sample conductivity
and its consequences are more pronounced on the capacitance than the conductance
of ionic solutions as well as biological samples (Schwan 1992). In the
case of biological samples, the poorly conducting cells shield part of
the electrode from the ionic current thus reducing the polarisation effects
compared to an ionic solution equivalent in conductivity to the intracellular
fluid. The material of the electrode plays an important part in determining
its polarisation impedance. In the current study gold plated and sputted
platinum electrodes were tested and a choice was made in favour of the
latter. The effect of the rough platinum surface was to shift the electrode
polarisation effect to lower frequencies and thus to reduce its contribution
in the frequency range under consideration. The inductance of the probe
and connecting cable add another series component to the measured impedance.
Its value could be determined from measurements on standard salt solutions
and applying an equivalent circuit analysis. For the present setup the
stray inductance is L=2x10-7 henry and the following equations
were used to account for it
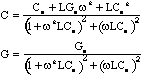
where C and G are the corrected capacitance and conductance expressed
in terms of the measured values Cm and Gm , the lead
inductance L and the angular frequency . The effect of the stray inductance
increases with frequency and with sample conductivity. Figures 1a and b
show the effect of electrode polarisation and the stray inductance on the
uncorrected permittivity and conductivity of a series of salt solutions
ranging from zero molar (deionised water) to 0.09 molar. The high permittivity
values at low frequencies are a manifestation of electrode polarisation
while negative permittivity values at high frequency show the effect of
the stray inductance. Superimposed on these data are the uncorrected permittivity
and conductivity of a tissue sample (heart tissue). It can be seen that
the low frequency conductivity of the tissue is less than that of 0.01
molar salt solution. It is therefore reasonable to assume that the effect
of electrode polarisation on the tissue is also less than that exhibited
by the 0.01 molar salt sample. A further observation indicates that the
errors in the permittivity and conductivity of the sample are likely to
be apparent below 1 kHz and significant below 100 Hz while the effect of
inductance manifests above a few megahertz in the case of tissue samples.
a. Permittivity
b. Conductivity
Figure 1. Uncorrected values of the permittivity and conductivity of a
series of salt solutions.
Also shown are the corrected and uncorrected data for heart tissue at 37oC.
To correct for electrode polarisation and induction errors the capacitance
and conductance of the tissue sample are evaluated in accordance with (2)
and normalised to a salt solution of similar low frequency conductivity.
The example in Figures 1a and b was corrected with reference to a 0.005
molar salt solution, the corrected dielectric properties are shown for
comparison purposes. All impedance analyser tissue measurements were treated
in a similar manner.
The measurement techniques and associated instrumentation used in this study give random reproducibility of about 1% across the frequency range. This statement is based on multiple measurements carried out on standard samples of uniform composition. Biological tissues are inhomogeneous and show considerable variability in structure or composition and hence in dielectric properties. Such variations are natural and may be due to physiological processes or other functional requirements. The spread of values ranges from about +/- 5% above 100 MHz to +/- 15% at the lower end of the frequency scale. Care has been taken to eliminate all known sources of systematic errors, however, in view of the assumptions made in correcting for electrode polarisation it is possible that the dielectric parameters below 1 kHz may be undercorrected. This source of errors may affect the dielectric parameters by up to a factor of two.
Three sources of materials were used:
All animal tissues were used as fresh as possible, mostly within two hours of death, human material was obtained 24 to 48 hours after death. The conical probe used in conjunction with the impedance analyser requires relatively large samples, at least a cube of 5 cm linear dimension. In view of this requirement not all samples could be measured at low frequencies.
Examples of measurements on the three experimental setup, across the frequency range are given in Appendix A (Figures A1 to A11). The agreement between measurements on the three machines was particularly good when the measurements were made on the same sample throughout. To achieve this objective the two network analysers and the impedance analyser were placed in close proximity to each other and interfaced to the same computer. All the measurement procedures were redesigned to operate through LabView(TM), a graphics interface medium from National Instruments running on an Intel Pentium microprocessor. In this arrangement, the measurements could be carried out on all three machines in quick succession. The dielectric properties of muscle are known to be anisotropic. The data reported were obtained by measurement on the paravertebral muscle. The sample was measured twice, first with a transverse section against the probe (Figure A9) and then it was cut along the muscle fibre and re-measured (Figure A10). In view of the radial nature of the fringing field of the coaxial probe these measurements do not represent the true limits of the dielectric properties with the field along and across the fibre. They show, however, the effect of fibre direction and the parts of the spectrum influenced by it. Human material could not be obtained in sufficient quantities for optimum measurements with the conical probe. Under such conditions the measurements on the impedance analyser were consistently lower than those obtained on the network analyser in the same frequency range. Examples of such measurements are given in Figures A12 to A15. Much smaller samples of human material were measured only in the frequency range above 1 MHz on the two impedance analysers. Examples of such measurements are given in Figures A16 to A19.
The differences in the dielectric properties of animal and human species
are not systematic. The variation in tissue properties within a species
may well exceed variations between species. Example of comparative measurements
are given in Figures 2 to 4.
Figure 2. Comparison between the dielectric properties of tongue muscle
from animal and human samples.
Figure 3. Comparison between the dielectric properties of tendon from two
animal species.
Figure 4. Comparison between the dielectric properties of small intestine
tissue from animal and human samples.
The dielectric properties of tissues have been extracted from the literature of the past five decades and compared to the corresponding data from the current study. The purpose is to provide an objective basis for the evaluation of the experimental data and to reach a broad based consensus on the subject. Reports of dielectric properties of tissues prior to 1950 are difficult to get hold of, they have more historical than practical interest and, with the exception of Osswald (1937), have not been reviewed. The literature in the 1950s and 60s is dominated by the work of H. P. Schwan and his collaborators and has been reviewed and tabulated by Durney et al 1986. Other extensive reviews include Geddes and Baker (1967) who summarised the early reports on the specific resistance of tissues, Stuchly and Stuchly (1980) who tabulated the dielectric properties of tissues in the frequency range 10 kHz to 10 GHz, Foster and Schwan (1989) who provided a wide historical perspective and Duck (1990) who extended their survey by including more recent data. In the current survey, data that correspond more closely to living human tissues were selected in preference to any other. Consequently, human tissue and in vivo measurements were selected in preference to animal tissue and in vitro measurements. For in vitro measurements, data obtained at temperatures closest to that of the body and nearest to the time after death were used when available. Most of the literature data were in graphical rather than table form and in a logarithmic rather than linear format. Such data were retrieved at each decade. When tables were available, a more extensive frequency range was often provided. The data were translated from the various authors' preferred set of parameters and units to relative permittivity and conductivity expressed in S/m. Data obtained at temperature as low as 20oC are included in this survey. It was not considered advisable to translate them to body temperature. The temperature coefficients, for both permittivity and conductivity, are tissue-type and frequency dependent. Information on these coefficients is scarce and not sufficiently robust to warrant generalisation and extrapolation. Moreover, the coefficients are highest (~1-2 %/oC) at low frequencies where the uncertainty and the scatter in the data are of a similar or higher order of magnitude than the differences due to a 10 or 15oC.
The data are presented in Appendix B in tabular as well as graphical formats. Details of the tissue-type, animal species, measurement temperature and the reference are included in the legend. To facilitate the comparison, the same scale was used for all tissues except where the conductivity of the tissue falls below 10-2 S/m. The references from which data were extracted are included in Appendix B.
One of the aims of this project is to derive models for the frequency
dependence of the dielectric properties of the tissues investigated. The
basis of the analysis is well known dispersions in the dielectric spectrum
of biological materials and their expression as a summation of terms corresponding
to the main polarisation mechanisms. The spectrum extends from Hz to GHz
and shows 4 dispersion regions. The complexity of the structure and composition
of biological material is such that each dispersion region is broadened
by multiple contributions to it and could be described by a Cole-Cole expression.
The model corresponding to the whole spectrum
(3)
in which, is
the permittivity in the terahertz frequency range,
is
the ionic conductivity, for each dispersion region
is the relaxation time and
is
the drop in permittivity in the frequency range corresponding to
.
With a choice of parameters appropriate to each tissue, (3) could be used
to predict its dielectric behaviour over the desired frequency range. The
parameters of the model were adjusted to correspond to a close fit between
the model and the most comprehensive data set available for the particular
tissue. The 4-Cole-Cole model describes the frequency dependence of the
dielectric properties in the frequency range from Hz to GHz. It can be
used with confidence for frequencies above 1 MHz. At lower frequencies,
where the literature values are scarce and have larger than average uncertainties,
the model should be used with caution in the knowledge that it provides
a 'best estimate' based on present knowledge. It is important to stress
the limitations of the model particularly where there are no data at all
to support its predictions. The 4-Cole-Cole analysis was carried out on
44 tissue types, the results are presented in a self explanatory manner
in Appendix C, the experimental data are tabulated in Appendix D.
Below 100 Hz the impedance of biological material is mostly resistive. The contribution of the capacitive component is of the order of 10 % in most cases. The literature surveyed in this study shows that there are wide variations in the conductivity values obtained for the same tissue in various studies. The contribution of the tissue permittivity to body current is well within the uncertainty associated with the corresponding tissue conductivity. Therefore, in practice, the estimation of induced current in tissue is based on such conductivity values. Table 1 gives an estimate for conductivity in S/m of the main body tissues below 100 Hz from this study mitigated by literature values. The values tabulated by Duck (1990) are also shown for comparison . Average values were used where appropriate.
The values obtained from this study were used to calculate the conductivity
of the whole and various parts of the body (Table 2). The necessary integration
of the conductivity of tissue to obtain values in table 2 were carried
out by allocating the appropriate values to a voxel anatomical human model
developed at The National Radiological Protection Board (NRPB) to aid dosimetry
work. The model known as NORMAN (normal man) will be described in a future
NRPB publication. The results of such an integration carried out at 10
and 100 kHz has also been included for comparison purposes.
Table 1: Estimates of the conductivity (S/m) of body
tissues below 100 Hz at body temperature.
|
Tissue |
From Duck 1990 |
This study |
|
Bladder |
0.2 |
|
|
Bone -Cancellous |
0.07 |
|
|
Bone -Marrow |
0.05 |
|
|
Cartilage |
0.18 |
|
|
Cerebro Spinal Fluid |
1.81 |
2.0 |
|
Cornea |
0.4 |
|
|
Fat |
0.04 |
|
|
Gall Bladder Bile |
1.6 |
1.4 |
|
Heart |
0.2 |
0.1 |
|
Lens |
0.25 |
|
|
Lung -Deflated |
0.1 |
0.2 |
|
Muscle |
0.4 |
0.35 |
|
Pancreas |
0.13 |
0.22 |
|
Small Intestine |
0.5 |
|
|
Stomach |
0.5 |
|
|
Testis |
0.4 |
|
|
Tongue |
0.3 |
|
|
Blood |
0.68 |
0.7 |
|
Bone -Cortical |
0.02 |
0.02 |
|
Breast |
0.06 |
|
|
Cerebellum |
0.1 |
|
|
Colon |
0.1 |
|
|
Dura |
0.5 |
|
|
White matter |
0.1 |
0.06 |
|
Grey Matter |
0.3 |
0.1 |
|
Kidney |
0.9 |
0.1 |
|
Liver |
0.12 |
0.07 |
|
Lung -Inflated |
0.05 |
0.08 |
|
Nerve |
0.4 |
0.03 |
|
Skin -Wet |
0.1 |
|
|
Spleen |
0.1 |
|
|
Tendon |
0.3 |
|
|
Urine |
3.3 |
|
|
Vitreous Humour |
1.5 |
|
|
Thyroid |
0.5 |
Table 2: Conductivity, in S/m, of the whole and parts
of the body obtained by integrating the conductivity values in Table 1
over various parts of the body
| Whole body | Head | Torso | Arm | Leg | Neck | |
| 50 Hz | 0.216 | 0.254 | 0.223 | 0.195 | 0.196 | |
| 10 kHz | 0.276 | 0.285 | 0.256 | 0.238 | 0.222 | |
| 100 kHz | 0.288 | 0.30 | 0.332 | 0.239 | 0.243 |
The main purpose of this project is to compile a database of dielectric
properties of tissues for use by the scientific community in solving electromagnetic
interaction problems. This has been achieved through measurement in the
frequency rang 10 Hz to 20 GHz and modelling the frequency dependence of
the dielectric properties of over 30 body tissues to parametric expressions
for inclusion in numerical solutions.
C Gabriel, T Y A Chan and E H Grant, "Admittance models for open
ended coaxial probes and their place in dielectric spectroscopy",
Physics in Medicine and Biology, 39, 12, 2183-2200, 1994.
Gabriel and E.H. Grant, "Dielectric sensors for industrial microwave
measurements and control", Microwellen und HF Magazin, vol 15, pp
643-645, 1989.
P. Schwan, "Linear and nonlinear electrode polarisation and biological
materials" Annals of Biomedical Engineering: 20, 269-288, 1992.
Durney, C.H., Massoudi, H. and Iskander, M.F., 1986, Radiofrequency radiation
dosimetry handbook, Brooks Air Force Base- USAFSAM-TR-85-73 , .
Geddes, L. A. and Barker, L. E., 1967, The specific resistance of biological
material - a compendium of data for the biomedical engineer and physiologist.,
Medical and Biological Engineering, 5, 271-293.
Stuchly, M. A. and Stuchly, S. S., 1980, Dielectric properties of biological
substances - tabulated, Journal of Microwave Power, 15, 1, 19-26.
Foster, K. R. and Schwan, H. P., 1989, Dielectric properties of tissues
and biological materials: A critical review, Critical Reviews in Biomedical
Engineering, 17, 1, 25-104.
Duck, F. A., 1990, Physical properties of tissue:A comprehensive reference
book, Academic Press, Harcourt Brace Jovanovich, Publishers.
TITLE
PAGE: Links and information.
APPENDIX
A: Experimental data.
APPENDIX
B1: Literature Survey. (Graphs)
APPENDIX
B2: Literature Survey. (Data)
APPENDIX
C: Modelling the frequency dependence of the dielectric properties to a
4 dispersions spectrum.
APPENDIX
D: Tabulation of the experimental data referred to in Appendix C.