 |
Radiofrequency Radiation
|
 |
Radiofrequency Radiation
|
 ) and conductivity (
) and conductivity (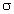 ).
Both properties change with temperature and, strongly, with
frequency. As a matter of fact, as the frequency increases
from a few hertz to gigahertz, the dielectric constant
decreases from several million to only a few units;
concurrently, the conductivity increases from a few millimhos
per centimeter to nearly a thousand.
).
Both properties change with temperature and, strongly, with
frequency. As a matter of fact, as the frequency increases
from a few hertz to gigahertz, the dielectric constant
decreases from several million to only a few units;
concurrently, the conductivity increases from a few millimhos
per centimeter to nearly a thousand.
 ,
,  , and
, and 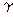 --of the dielectric constant at low,
medium, and very high frequencies. In its simplest form each
of these relaxation regions is characterized by equations of
the Debye type as follows,
--of the dielectric constant at low,
medium, and very high frequencies. In its simplest form each
of these relaxation regions is characterized by equations of
the Debye type as follows,
 ,
,  , and
, and 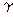 dispersions. They include for the
dispersions. They include for the  -effect, apparent membrane property changes as described in the text; for the
-effect, apparent membrane property changes as described in the text; for the  -effect, tissue structure (Maxwell-Wagner effect); and for the
-effect, tissue structure (Maxwell-Wagner effect); and for the 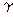 -effect, polarity of the water molecule (Debye effect). Fine structural effects are responsible for deviations as indicated by the dashed lines. These include contributions from subcellular organelles, proteins, and counterion relation effects.
-effect, polarity of the water molecule (Debye effect). Fine structural effects are responsible for deviations as indicated by the dashed lines. These include contributions from subcellular organelles, proteins, and counterion relation effects. (Equation 4.1)
(Equation 4.1) -dispersion
effect. Rotation of molecules having a permanent dipole
moment, such as water and proteins, is responsible for the
-dispersion
effect. Rotation of molecules having a permanent dipole
moment, such as water and proteins, is responsible for the
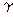 -dispersion (water) and a small addition to the tail of the
-dispersion (water) and a small addition to the tail of the
 -dispersion. The plot does not include the
-dispersion. The plot does not include the 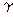 -dispersion.
-dispersion.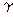 -dispersion is due solely to water and its
relaxational behavior near about 20 GHz. A minor additional
relaxation (
-dispersion is due solely to water and its
relaxational behavior near about 20 GHz. A minor additional
relaxation ( 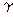 -dispersion is caused in part
by rotation of amino acids, partial rotation of charged side
groups of proteins, and relaxation of protein-bound water
which occurs somewhere between 300 and 2000 MHz.
-dispersion is caused in part
by rotation of amino acids, partial rotation of charged side
groups of proteins, and relaxation of protein-bound water
which occurs somewhere between 300 and 2000 MHz.
 -dispersion is presently the least clarified.
Intracellular structures, such as the tubular apparatus in
muscle cells, that connect with the outer cell membranes
could be responsible in tissues that contain such cell
structures. Relaxation of counterions about the charged
cellular surface is another mechanism we suggest. Last but
not least, relaxational behavior of membranes per se, such as
reported for the giant squid axon membrane, can account for
the
-dispersion is presently the least clarified.
Intracellular structures, such as the tubular apparatus in
muscle cells, that connect with the outer cell membranes
could be responsible in tissues that contain such cell
structures. Relaxation of counterions about the charged
cellular surface is another mechanism we suggest. Last but
not least, relaxational behavior of membranes per se, such as
reported for the giant squid axon membrane, can account for
the  -dispersion (Takashima and Schwan, 1974). The relative
contribution of the various mechanisms varies, no doubt, from
one case to another and needs further elaboration.
-dispersion (Takashima and Schwan, 1974). The relative
contribution of the various mechanisms varies, no doubt, from
one case to another and needs further elaboration.
 ,
, 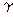 , and
, and  -dispersion centered at about 2 kHz, while
muscle displays a very strong one near 0.1 kHz. The
-dispersion centered at about 2 kHz, while
muscle displays a very strong one near 0.1 kHz. The
 - and
- and 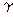 -dispersion, however, is always sharply defined at the same
frequency range.
-dispersion, however, is always sharply defined at the same
frequency range.
 -,
-, 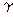 -Dispersion Effects
-Dispersion Effects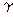 -dispersion characteristic of water. To the water's
-dispersion characteristic of water. To the water's
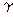 -dispersion, biological macromolecules add a
-dispersion, biological macromolecules add a  -range
as indicated. Suspensions of cells free of protein would
display a Maxwell-Wagner
-range
as indicated. Suspensions of cells free of protein would
display a Maxwell-Wagner 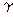 -dispersion of water. If the cells contain protein an additional,
comparatively weak
-dispersion of water. If the cells contain protein an additional,
comparatively weak  -mechanism due to counterion relaxation is
added; and if their membranes relax on their own as some excitable membranes
do, an additional mechanism may appear.
-mechanism due to counterion relaxation is
added; and if their membranes relax on their own as some excitable membranes
do, an additional mechanism may appear.
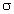 s term
in Equation 4.1 due to the ionic conductance of the dissolved
ion species. The static dielectric permittivity of
electrolytes of usual physiological strength (0.15 N) is
about two units lower than that of pure water (Hasted, 1963),
a negligible change.
s term
in Equation 4.1 due to the ionic conductance of the dissolved
ion species. The static dielectric permittivity of
electrolytes of usual physiological strength (0.15 N) is
about two units lower than that of pure water (Hasted, 1963),
a negligible change.
 s, observed at f << fc = 20 GHz
s, observed at f << fc = 20 GHz
 (Equation 4.2)
(Equation 4.2)
 (Equation 4.3)
(Equation 4.3)
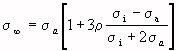 (Equation 4.4)
(Equation 4.4)
for the limit values of the simple dispersion that characterizes the frequency dependence. The time constant is
 (Equation 4.5)
(Equation 4.5)
In these equations, Cm and G m are capacitance and
conductance per square centimeter of the cell membrane; R is
the cell radius; ![]() is the cellular volume fraction, and
is the cellular volume fraction, and ![]() i =
1/
i =
1/![]() i and
i and ![]() a = l/
a = l/![]() a are the conductivities of the cell
interior and suspending medium. The equations apply for
small-volume fractions,
a are the conductivities of the cell
interior and suspending medium. The equations apply for
small-volume fractions, ![]() , and assume that the radius of the
cell is very large compared with the membrane thickness. More
elaborate closed-form expressions have been developed for
cases when these assumptions are no longer valid (Schwan and
Morowitz, 1962; Schwan et al., 1970), and an exact
representation of the suspension dielectric properties as a
sum of two dispersions is available (Pauly and Schwan, 1959).
If, as is usually the case, the membrane conductance is
sufficiently low, Equations 4.2-4.5 reduce to the simple
forms to the right of the arrows.
, and assume that the radius of the
cell is very large compared with the membrane thickness. More
elaborate closed-form expressions have been developed for
cases when these assumptions are no longer valid (Schwan and
Morowitz, 1962; Schwan et al., 1970), and an exact
representation of the suspension dielectric properties as a
sum of two dispersions is available (Pauly and Schwan, 1959).
If, as is usually the case, the membrane conductance is
sufficiently low, Equations 4.2-4.5 reduce to the simple
forms to the right of the arrows.
 , which determines the frequency where the impedances 1/
, which determines the frequency where the impedances 1/ CmR and (
CmR and ( s -
s - 
 , is exceptionally high.
, is exceptionally high.
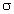 s,
s, 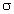
 ,
,
 s -
s - 
 ), and
), and  , the three quantities Cm,
, the three quantities Cm,  Cm, is about 0.5
Cm, is about 0.5 Go to Chapter 4.1.2
Return to Table of Contents.
Last modified: June 24, 1997
© October 1986, USAF School of Aerospace Medicine, Aerospace Medical Division (AFSC), Brooks Air Force Base, TX 78235-5301