 |
Radiofrequency Radiation
|
|
Radiofrequency Radiation
|
This chapter was revised by Eleanor R. Adair, Ph.D., Associate Fellow, John B. Pierce Foundation Laboratory, Yale University. It includes material written by James L. Lords, Ph.D., and David K. Ryser, Ph.D., from previous editions of this handbook and new material added by Dr. Adair.
The study of thermoregulation--the responses that maintain a constant internal body temperature--has flourished since Claude Bernard (1865) first demonstrated that the temperature of the blood varies in different parts of the body. Bernard established that food taken into the body is metabolized in the tissues and that the bloodstream distributes the released energy throughout the body. The relative constancy of the internal body temperature was part of his concept of the constancy of the milieu intérieur, a necessity for optimal functioning and health of the organism. He pointed out that the vasomotor nerves control the transfer of heat from deep in the body to the skin and that this is a mechanism of the utmost importance to thermoregulation in homeotherms. Bernard's discoveries underlie the modern science of thermophysiology and help us to understand how man and animals can remain relatively independent of the thermal environment, even when that environment contains potent or unusual thermal stressors.
Thermal loads on the body can result from changes in metabolic heat production and from changes in the characteristics of the environment (temperature, ambient vapor pressure, air movement, insulation, and other environmental variables that may alter the skin's temperature), Thermalizing energy deposited in body tissues by exposure to radiofrequency electromagnetic radiation can be a unique exception to the normal energy flows in the body, although metabolic activity in skeletal muscle can deposit large amounts of thermal energy directly into deep tissues.
All living organisms respond vigorously to changes in body temperature. Cold-blooded animals, called ectotherms because they derive thermal energy mainly from outside the body, regulate their body temperatures largely through behavioral selection of a preferred microclimate. Warm-blooded animals, called endotherms because they can produce heat in their bodies and dissipate it to the environment through physiological processes, often rely largely on behavioral thermoregulation. Behavior is important to thermoregulation because it is mobilized rapidly and aids the conservation of body energy and fluid stores. When behavioral responses--which include the thermostatic control of the immediate microenvironment--are difficult or impossible, the body temperature of endothermic species is regulated by the autonomic mechanisms that control heat production, the distribution of heat within the body, and the avenues and rate of heat loss from the body to the environment.
Other descriptive terms currently used include "temperature conformer" for ectotherm and "temperature regulator" for endotherm. Some thermal physiologists prefer a different classification, based on the quality of the thermoregulation: A homeotherm normally regulates its body temperature within rather narrow limits by varying its metabolic rate, heat and moisture loss, or position in the environment; a poikilotherm may allow its body temperature to vary over a considerable range, and regulates that variation by its position in the environment. Complications for the latter scheme arise when one considers hibernators (endotherms that periodically become poikilothermic) or ectotherms that are effectively homeothermic by virtue of efficient behavioral thermoregulation. The terms "endotherm" and "ectotherm" are used in the material that follows.
Radiofrequency radiation may be regarded conveniently as
part of the thermal environment to which man and other
endotherms may be exposed. Figure 10.1 is a schematic
representation of the sources of heat in the body and of the
different routes by which thermal energy may be transferred
between the body and the environment. Heat is produced in the
body through metabolic processes (M) and may also be
passively generated in body tissues by absorption of RFR
(
).
If the body temperature is to remain stable, this
thermal energy must be continually transferred to the
environment. As outlined above, the balance between the
production and loss of thermal energy is so regulated by
behavioral and autonomic responses that minimal variation
occurs in the body temperature of an endotherm.
Energy may be lost (Figure 10.1) by evaporation of water
from the respiratory tract (
)
or from the skin (
), by
dry-heat transfer from the skin surface via radiation (
) or
convection (
), and by doing work (W = force x distance) on
the environment. Heat transfer by conduction is usually
insignificant in most species unless they are recumbent. When
the environment is thermally neutral, dry-heat loss
predominates in the form of convective transfer to the air
and radiant transfer to the surrounding surfaces. A small
amount of heat is always lost by the diffusion of water
through the skin (not shown in the figure).
When the temperature of the environment rises above
thermoneutrality, or during vigorous exercise or
defervescence, the evaporation of sweat () dissipates
large amounts of body heat. Evaporative water loss through
sweating occurs in man, the great apes, certain other
primates, and a few other species such as horses and camels.
Many animals--such as dogs, cats, and rabbits--use panting
(increased respiratory frequency coupled with copious saliva
production) to lose heat by evaporation. Other species, such
as the rodents, have no such physiological mechanisms and
must rely on behavioral responses which include seeking
shade, burrows, or aqueous environments and/or grooming their
bodies with water, urine, or saliva to aid evaporative
cooling. Table 10.1 includes several thermoregulatory
characteristics of certain animals.
The rate of heat loss from an endotherm is governed by
the thermal characteristics of the environment, as indicated
in Figure 10.1; these include not only the air temperature
(
) but also the air movement (v) and humidity (RH). Two
other environmental variables that affect heat transfer (not
shown in the figure) are the mean radiant temperature of
surrounding surfaces , especially those close to the body,
and the amounts of insulation (fur, fat, feathers,
clothing).
When the thermal energy produced in the body (including that derived from absorbed RFR) is equal to that exchanged with the environment, the body is said to be in thermal balance. Under these conditions the body temperature remains stable. When heat production exceeds heat dissipation, thermal energy is stored in the body and the body temperature rises (hyperthermia). On the other hand, when more heat is transferred to the environment than can be produced or absorbed, the body temperature falls (hypothermia).
The particular thermoregulatory effector response mobilized at any given time, and its vigor, will depend on the prevailing thermal environment. The ambient temperature is frequently the only environmental variable specified in research reports, but the specification of air movement and relative humidity is equally important. Figure 10.2, a schematic thermoregulatory profile of a typical endotherm, illustrates how the principal autonomic responses of heat production and heat loss depend on the ambient temperature. The responses are considered to be steady state rather than transient, and the ambient air is considered to have minimal movement and water content. Three distinct zones can be defined in terms of the prevailing autonomic adjustment. Below the lower critical temperature (LCT), thermoregulation is accomplished by changes in metabolic heat production, other responses remaining at minimal strength . As the ambient temperature falls further and further below the LCT, heat production increases proportionately. In a cool environment RF energy absorbed by an endotherm will spare the metabolic system in proportion to the field strength and will have no effect on other autonomic responses.
At ambient temperatures above the LCT, metabolic heat production is at the low resting level characteristic of the species, evaporative heat loss is minimal, and changes in thermal conductance accomplish thermoregulation. Conductance is a measure of heat flow from the body core to the skin and reflects the vasomotor tone of the peripheral vasculature. As the constricted peripheral vessels begin to dilate, warm blood from the body core is brought to the surface so that the heat may be lost to the environment by radiation and convection. These vasomotor adjustments take place within a range of ambient temperatures, called the thermoneutral zone (TNZ), that is peculiar to each species. Insofar as they are known, the TNZs for animals commonly used in the laboratory are indicated in Table 10.1. If an endotherm at thermoneutrality is exposed to RFR, augmented vasodilation may occur so that the heat generated in deep tissues can be quickly brought to the skin surface for dissipation to the environment.
The upper limit of the TNZ is known as the upper critical temperature (UCT). At this ambient temperature the endotherm is fully vasodilated and
dry-heat loss (by convection and radiation) is maximal. Further increases in ambient temperature provoke the mobilization of heat loss by evaporation, either from the skin (sweating) or the respiratory tract (panting). Man and certain other mammals have the ability to sweat copiously to achieve thermoregulation in hot environments. It is reasonable to assume that if these species were exposed to RFR at ambient temperatures above the UCT, their sweating rate would increase in proportion to the field strength. Other mammals, notably the rodents, neither sweat nor pant and when heat stressed must depend on behavioral maneuvers to achieve some degree of thermoregulation; if the opportunity for behavioral thermoregulation is curtailed, these animals can rapidly become hyperthermic when heat stressed. The basic thermoregulatory profile of the selected laboratory animal must therefore be considered in detail as part of the experimental design of any research into the biological consequences of exposure to RFR; changes in any measured thermoregulatory response will depend on the functional relationship between that response and the prevailing ambient temperature. Other types of responses also may be indirectly affected by the thermoregulatory profile if they interfere with efficient thermoregulation (e.g., food and water consumption).
Man exhibits profound adaptability in the face of environmental thermal stress, particularly in warm environments. Figure 10.3 illustrates some of the fundamental data collected by Hardy and DuBois (1941) for nude men and women exposed in a calorimeter to a wide range of ambient temperature Because of the vigorous responses of heat production and heat loss, the rectal temperature varies less than 1ºC across a 20ºC range of calorimeter temperature. The TNZ is extremely narrow, occurring at about 28ºC in the calorimeter and closer to 30ºC in the natural environment. Above the TNZ, evaporative heat loss (whole-body sweating) is initiated that can attain rates of 2-3 L/h and up to 10-15 L/d (Wenger, 1983). Assuming normal hydration, it is difficult to increase metabolic heat production (by exercise) to levels that cannot be dissipated by sweating, unless the ambient temperature or vapor pressure is very high. Since human evaporative heat loss is controlled by both peripheral and internal thermal signals (Nadel et al., 1971), only an extraordinarily hostile thermal environment, which includes a source of RFR, can be expected to seriously threaten man's thermoregulatory system.
Way et al. (1981) and others (Stolwijk, 1983) have predicted minimal increases in brain and body temperatures during local absorption of significant amounts of RF energy, because of the rapid mobilization of evaporative heat loss and a significant increase in tissue blood flow. Under the assumption that RF exposure provides a thermal stress comparable to exercise (Nielsen and Nielsen, 1965) or an ambient temperature well above the TNZ, such response changes would be predicted from knowledge of the human thermoregulatory profile in Figure 10.3. On the other hand, significant temperature elevations in certain body sites (e.g., the legs, arms, and neck) have been predicted by a two-dimensional heat-transfer model of man exposed to a unilateral planewave at resonant and near-resonant frequencies (Spiegel et al., 1980). These predictions should be verified in animal models or, preferably, in human subjects exposed to comparable fields.
The most important principle involved in the study of autonomic thermoregulation of endotherms is the first law of thermodynamics--the law of conservation of energy (Bligh and Johnson, 1973). In the steady state the heat produced in the body is balanced by the heat lost to the environment, so heat storage is minimal. This relationship can be expressed by a heat-balance equation:
M ± W = R + C + E ± S (Equation 10.1)
in which
M = rate at which thermal energy is produced through metabolic processes
W = power, or rate at which work is produced by or on the body
R = heat exchange with the environment via radiation
C = heat exchange with the environment via convection
E = rate of heat loss due to the evaporation of body water
S = rate of heat storage in the body
All terms in Equation 10.1 must be in the same units, e.g. , watts (the unit used throughout this handbook). Physiologists commonly express these quantities in kilocalories per hour, which can be converted to watts by multiplying by 1.163, the conversion factor. As Equation 10.1 is written, negative values of R, C, and E may all cause a rise in the body temperature; positive values may cause a fall. Work (W) is positive when accomplished by the body (e.g., riding a bicycle), and this potential energy must be subtracted from metabolic energy (M) to find the net heat (H) developed within the body. When W is negative (e.g., walking downstairs), this heat is added to M. While W may be a significant factor for humans or beasts of burden, it may be considered negligible for other endotherms, particularly in a laboratory setting. Usually evaporative heat loss (E) is positive; when E is negative, condensation occurs and thermal injury is possible.
Because heat exchange by radiation, convection, or evaporation is always related in some way to the surface area of the body, each term in Equation 10.1 is usually expressed in terms of energy per unit surface area, e.g., watts per square meter. The most commonly used measure of the body surface area of humans is that proposed by DuBois (1916),
(Equation 10.2)
where
= DuBois surface in square meters
w = body mass in kilograms
h = height in meters
As noted by Kleiber (1961), h for similar body shapes is
proportional to a mean linear dimension equal to 
.
Therefore, to compare humans of different sizes, Equation
10.2 may be generalized as
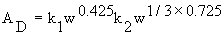
(Equation 10.3)The ratio of surface area to body mass varies between
species, so it is difficult to establish a general rule for
the determination of surface area. Many methods have been
devised for the direct measurement of the surface area of
experimental animals, most of which are inaccurate to some
degree. In nearly all cases, the surface area is some
function of 
.
Although Equation 10.1 has no term for heat transfer
through conduction (which is usually insignificant under
normal conditions), conduction combined with mass transfer
forms the significant mode of heat transfer called
convection. Convective heat transfer in air (C) is a linear
function of body surface area (A), and the convective heat
transfer coefficient (
) is a function of ambient air
motion to the 0.6 power (
) The amount of heat the body
loses through convection depends on the difference between
the surface temperature of the skin (
) and the air
temperature, usually taken as the dry-bulb temperature (
).
The value of the heat-transfer coefficient depends on certain
properties of the surrounding medium, such as density and
viscosity, as well as a shape/dimension factor for the body.
Clothing complicates the analysis and is often evaluated in
terms of insulation (clo) units.
Heat transfer by radiation is independent of ambient
temperature. The wavelengths of the radiation exchanged
between two objects are related to their respective surface
temperatures; the net heat transfer by radiation is
proportional to the difference between their absolute
temperatures to the fourth power and to the relative
absorptive and reflective properties of the two surfaces. In
general, the net radiant-heat exchange (where 
=
radiant-heat-transfer coefficient) between a nude man and the
environment involve a estimation of the mean radiant
temperature (MRT). MRT (alternate symbol 
) can be derived
from the temperature (
) of a blackened hollow sphere of
thin copper (usually 0.15-m diameter) having heat-transfer
characteristics similar to those for the human body (Woodcock
et al., 1960):
(Equation 10.4)
Clothing complicates this analysis as it does heat transfer by other modes. Heating by RFR may further complicate the analysis of radiant-heat exchange between a man and his environment, although Berglund (1983) has demonstrated that this complex situation can be analyzed by conventional methods.
The final avenue of heat loss available to man is that
due to the evaporation of water. The latent heat of
vaporization of water at normal body temperature is 0.58
kcal/g; the body loses this amount of heat when water is
evaporated from its surfaces. Water from the respiratory
surfaces is continually being lost in the expired air. Water
also continually diffuses through the skin; this is called
insensible water loss or insensible perspiration. These two
avenues contribute equally to a heat loss that totals about
25% of the resting metabolic heat production of a man in a
thermoneutral environment. However, the major avenue of
evaporative heat loss in man is sweating, which depends on
the vapor pressures of the air and the evaporating surface
and is thus a direct function of both dry bulb () and wet
bulb (
)
temperatures. When 
, the air is at 100%
relative humidity and thus no water can be evaporated from
the skin surface; at less than 100% relative humidity,
evaporation can occur. The interrelationships between these
variables can be determined from a standard psychrometric
chart (ASHRAE Handbook, 1981). In Equation 10.1, E represents
the evaporative cooling allowed by the environment (
)
and is in no way related to the level of evaporative cooling
required (
) by the man.
Because the metabolic heat production per unit body mass, or "Specific metabolic rate," varies greatly with body size and proportion (somatotype), several measures of this variable are in wide use. Figure 10.4 is a log-log plot of metabolic heat production versus body mass for several animals and man. The solid line with a slope of 0.75 reveals a strong correlation between body mass raised to the 0.75 power and metabolic heat production. This empirical observation has prompted researchers to adopt power per unit body mass, in units of watts per kilogram, as the standard metric for animal metabolic rate.
The metabolic heat production (M) of placental animals (most mammals) can be estimated by the following formula:
(Equation 10.5)
where w is the mass of the animal in kilograms. Another useful equation relates the metabolic heat produced by the body to the rate of oxygen consumption (ASHRAE Handbook, 1981):
(Equation 10.6)where
RQ = the respiratory quotient, or ratio of 
produced
to 
inhaled; RQ in man may vary from 0.83 (resting ) to over
1.0 ( heavy exercise)
= oxygen consumption in liters/minute at
standard conditions (O°C 760 mmHg)
5.87 = the energy equivalent of 1 L of oxygen at standard conditions in watt-hours/liter when RQ = 1.
Formulas for the metabolic heat production of other classes of animals can be found in an article by Gordon (1977).
Another widely accepted form for expressing metabolic heat production is power per unit surface area. The dashed line in Figure 10.4, with a slope of 0.67, represents how surface area increases with mass for geometrically similar shapes. This corresponds to the approximate formula for the body surface area (SA) of these animals:
(Equation 10.7)
Although surface area does not describe the
animal data as well as 
,
it is as suitable a measure as
any for human metabolic heat production. For accurate
calculations of human metabolic heat production, the DuBois
area (Equation 10.2) should be used.
Metabolic heat production (M) is often called "metabolic rate" (MR). Table 10.2 lists resting metabolic rates for normal healthy humans of varying age and somatotype. The specific metabolic rate (SMR; W/kg) is clearly seen to be a function of body size and shape.
The basal metabolic rate (BMR) is defined as the heat
production of a human in a thermoneutral environment
(33ºC), at rest mentally and physically and at a time
exceeding 12 h from the last meal. The standard BMR for man
is about 250 ml 
, or 84 W, or 0.8 MET (where 1 MET =
58.2 W/m² ). The BMR also corresponds to about 1.2 W/kg
for a 70-kg "standard" man. The BMR is altered by
changes in active body mass, diet, and endocrine levels but
probably not by living in the heat (Goldman, 1983). In
resting man most of the heat is generated in the core of the
body--the trunk, viscera, and brain-despite the fact that
these regions represent only about one-third of the total
body mass. This heat is conducted to the other body tissues,
and its elimination from the body is controlled by the
peripheral vasomotor system.
Table 10.3 shows the wide variation of metabolic rates during various activities. All of these data are given for a healthy normal 20- to 24-yr-old male except as noted. The range of metabolic rate for humans--considering work performed and assorted physiological variables such as age, sex, and size--is roughly 40 to 800 W/m² (1 to 21 W/kg for "standard" man), depending on physical fitness and level of activity. The influence of age and sex on the metabolic rate of humans is shown in Figures 10.5 and 10.6. Other factors that may influence the metabolic rate are endocrine state, diet, race, pregnancy, time of day, and emotional state. If deep-body temperature is altered, from either heat storage in warm environments or febrile disease, a comparable change occurs in the metabolic rate (Stitt et al., 1974). Similar changes occur when deep-body temperature rises during exposure to RFR (Adair and Adams, 1982).
Resting metabolic rates (MR) for some adult laboratory animals are shown in Table 10.4 in three different forms: total MR for the weight given, specific MR, and standardized MR.
A rough idea of metabolic heat production can be gained
from an animal's oxygen consumption () by using the
formula
(Equation 10.8)
where = liters of oxygen consumed per
minute. The energy equivalent of oxygen is approximately 4.8
kcal/L 
for a typical animal diet, and the respiratory
quotient (RQ) is approximately 0.85.
Changes in vasomotor tonus and evaporation of body water through active sweating (or panting in certain endotherms) are both mechanisms of body heat loss. As detailed in Section 10.3 (Figures 10.2 and 10.3), vasomotor control normally operates to regulate the body temperature when an endotherm is in a thermoneutral environment, i.e., within the TNZ. Sweating (or panting) is activated in warmer environments and during exercise and defervescence.
Convective heat transfer via the circulatory system is controlled by the sympathetic nervous system. Below the LCT, vasoconstriction of the peripheral vasculature in arm, leg, and trunk skin minimizes heat loss from the skin, leaving a residual conductive heat flow of 5-9 W/m per ºC difference between body core and skin. For a body in the TNZ, when the peripheral vessels are vasodilated, each liter of blood at 37ºC that flows to the skin and returns 1ºC cooler allows the body to lose about 1 kcal, or 1.16 W•h, of heat (Hardy, 1978). During vigorous exercise in the heat, peripheral blood flow can increase almost tenfold; this increase is essential to eliminate the increased metabolic heat produced in the working muscles.
Tissue conductance (K) represents the combined effect of two channels of heat transfer in the body--conductive heat transfer through layers of muscle and fat and convective heat transfer by the blood. Tissue thermal conductance is defined as the rate of heat transfer per unit area during a steady state when a difference of 1ºC is maintained across a layer of tissue (W/m² • ºC) Johnson, 1973. Although K cannot be measured directly in the human organism, it can be estimated for resting humans under the assumption that all the heat is produced in the core of the body and is transferred to the skin and thence to the environment. Thus
(Equation 10.9)
in which 
represents the heat loss
(neglecting that lost through respiretion), Tre is rectal or
core temperature, and 
is the average skin temperature.
In the cold (22-28ºC), conductance is minimal for both
men and women, ranging between 6 and 9 W/m² •
ºC. In warm environments conductance increases rapidly,
and women show a faster increase than men (Cunningham, 1970;
also see Figure 10.3).
Evaporation of sweat from the skin surface efficiently removes heat even in environments warmer than the skin. In this case, evaporative heat loss must take care of both metabolic heat and that absorbed from the environment by radiation and convection. We have no reason to believe that thermalizing energy from absorbed RFR will be dealt with any differently than heat produced by normal metabolic processes or absorbed by exposure to warm environments.
Normal secretory functioning of the approximately 2.5 million sweat glands on the skin of a human being is essential to the prevention of dangerous hyperthermia. Secretion is controlled by the sympathetic nervous system and occurs when the ambient temperature rises above 30-31ºC or the body temperature rises above 37ºC. Local sweating rate also depends on the local skin temperature (Nadel et al., 1971). Physically fit individuals and those acclimated to warm environments sweat more efficiently and at a lower internal body temperature than normal (Nadel et al., 1974). Dehydration or increased salt intake will alter plasma volume and decrease sweating efficiency (Greenleaf, 1973).
The maximum sweat rate for humans and the length of time it can be maintained are limited. The maximum rate of sweat production by an average man is about 30 g/min. If the ambient air movement and humidity are low enough for all this sweat to be evaporated, the maximum cooling will be about 675 W/m²; however, conditions are not usually this ideal--some sweat may roll off the skin or be absorbed by layers of clothing. A more practical limit of cooling is 350 W/m², or 6 METS, which represents about 17 g/min for the average man (ASHRAE Handbook, 1981).
The operating characteristics of the thermoregulatory system appear to be similar to those of an automatic control system involving negative feedback. The body temperature of endotherms appears to be regulated at a set, or reference, level. Temperature sensors located in the skin and various other parts of the body detect temperature perturbations and transmit this information to a central integrator,or controller, that integrates the sensory information, compares the integrated signal with the set point, and generates an output command to the effector systems for heat production or loss. The responses thus mobilized tend to return the body temperature back to the set level.
These hypothetical constructs aid our understanding of thermoregulatory processes and let us formulate simulation models that can be used to predict human response to a wide variety of thermal stressors. Models have been of many types, from verbal descriptions to highly sophisticated electrical analogs and mathematical models. Hardy (1972) gives a comprehensive account of the development of modeling in thermal physiology. Many simulation models have been used to predict human responses to RFR (Farr et al., 1971). Of particular relevance are the theoretical models of Mumford (1969) and Guy et al. (1973) that use a heat-stress index to describe man's response to particular environmental and RF heat loads. A model by Emery et al. (1976b) uses several sweat rates to calculate the thermal response of the body to absorbed RFR. A model of Stolwijk and Hardy (1966) has been combined with simulations of RFR energy deposition by Stolwijk (1980) and Way et al. (1981) to demonstrate that the rise in local temperatures in the human body, especially in the brain, may be much less than anticipated during the localized deposition of RF energy, even when the radiation is focused on the hypothalamus. Greatly enhanced evaporative heat loss, skin blood flow, and conductance serve to protect individual body tissues during RFR energy deposition. On the other hand, a two-dimensional, combined RF-heat-transfer model developed by Spiegel et al. (1980) predicts rapid localized temperature increments in the thigh of a nude male resting at thermoneutrality and exposed to 80 MHz at 50 mW/cm², and similar temperature increments in the steady state at power densities as low as 10 mW/cm². Adding to this model the altered tissue blood flow for temperatures in excess of 40ºC may modify these predictions.
Much is known about the upper limits of human tolerance to hot, humid environments that contain no source of RFR (Givoni and Goldman, 1972; Proving et al., 1962). Knowing what the human tolerance time would be for a given SAR would be useful. This section describes calculations of the approximate SAR that will produce a critical internal body temperature in a standard man exposed for 60 min in a specified hot and humid environment.
The body's two physiological mechanisms that deal with heat stress, vasomotor and sudomotor, are each a complex function of many variables. The problem can be simplified, however, if we assume that the body is calling upon its maximum thermoregulatory capacity. Under most conditions of severe thermal stress, evaporative cooling is limited by the evaporation rate, not the sweat rate since the maximum sweat rate is over 2 L/h. If the psychrometric conditions (air temperature, relative humidity, and air velocity), skin temperature, and clothing characteristics are known, the heat storage in the body can be calculated by the fundamental heat-balance equation (10.1).
Agreement is not complete on the physiological criteria
that best describe the limits of human thermal tolerance.
Several researchers (Ellis et al., 1964; Craig et al., 1954;
Goldman et al., 1965; Wyndham et al., 1965) have used a
rectal temperature (
)
of 39.2ºC as a useful
criterion for setting the upper level of heat-stress
tolerance in clinical trials. Others
have advocated the use of more subjective criteria such
as faintness and loss of mental and physical ability (Bell
and Walters, 1969; Bell et al., 1965; Machle and Hatch,
1947). Since quantitative calculations based on such
subjective criteria are not practical, for the purposes of
the following calculations we have defined a of
39.2ºC as the danger level for man. With this
definition, the critical rate of heating for a 1-h period is
that which will cause a rise in of 2.2ºC/h,
assuming a normal beginning rectal temperature of 37ºC
and neglecting any temporal lag in the response.
We utilized data for the change in mean skin temperature
(
) as a function of time collected in an experiment
recorded by Ellis et al. (1964), in which a healthy 28-yr-old
male exposed to a hot, humid environment was judged by
observers to have reached his tolerance limit in 61 min. His
final rectal temperature was 39.4ºC. His skin
temperature rose bimodally from 36.9 to 38.4ºC during
the first 20 min of exposure, then increased more slowly to
39.3ºC in the next 41 min because of the onset of
sweating.
If these data for and
are assumed to be generally
true for a man heat stressed to his tolerance point in 1 h,
we should be able to calculate lesser amounts of heat storage
imposed on the body by less severe environmental conditions
that permit greater rates of evaporative cooling. Also,
substituting an equivalent amount of heat energy absorbed
during exposure to RFR for metabolic energy seems reasonable.
Such an equivalence was demonstrated by Nielsen and Nielsen
(1965) when they measured identical thermoregulatory
responses to exercise and to diathermic heating. This
assumption would be expected to be valid for RFR at
frequencies up to the postresonance region (perhaps up to
about 1 GHz for the average man), but might not be valid at
higher frequencies where the RFR causes primarily surface
heating. Consequently, the results calculated in the next
section are restricted to radiation conditions where the RF
heating does not occur primarily on the surface. The
substituted equivalent RFR heat load, expressed in watts per
kilogram of body mass, is designated the 
--the specific
absorption rate that would produce a rectal temperature of
39.2ºC in the irradiated subject in 60 min. The is
intended to represent the maximum SAR that a healthy average
man can tolerate, with regard to thermal considerations
alone, for 60 min in a given environment, assuming both that
the capacity to thermoregulate is
normal and that the other criteria for metabolic rate,
posture, clothing, and behavior specified below are
valid.
For the following calculations the required parameters for man and the environment are listed in Table 10.5. Standard values obtained from physiology texts (Kerslake, 1972; Mountcastle, 1974; Newburgh, 1949; Ruch and Patton, 1973) are given for the sample calculations. The symbols, units, and conversion factors used in this section conform for the most part to the uniform standards proposed by Gagge et al. (1969).
The calculations are based on a modification of the fundamental heatbalance equation (10.1) which neglects the work factor (W), groups together the terms for dry-heat losses (R + C), and incorporates the electromagnetic power absorbed (P):
M + P = (R + C) + E + S
or
S = M - (R + C) - E + P (Equation 10.10)
in which all symbols are as previously defined. The total heat load is given
by
(Equation 10.11)where 
is the change in rectal temperature caused by
heat load H. The evaporation rate is given by
(Equation 10.12)The dry-heat losses due to radiation and convection can be represented by
(Equation 10.13)Combining Equations 10.10, 10.12, and 10.13 and using values from Table 10.5 results in
(Equation 10.14)
This equation is first solved for the particular psychrometric conditions of interest with no RF power absorbed (P = 0). Over a 1-h period, the heat load due to the environment alone is given by
(Equation 10.15)The solution is -60 kcal when 
and 
. By Equation 10.11, the heat load that causes a
2.2ºC rise in was 128 kcal for this particular
man.
The power, P, that will cause a 2.2ºC rise in in
1 h is the difference between H and 128 kcal.
P = 218 W
The is simply
By using the SAR curves for an average man, we
can plot the incident power density that will produce the
for any given frequency and polarization, as shown in
Figure 10.7. The calculated values plotted on this
graph represent the worst possible case for man, which is,
according to the data for the prolate spheroidal model, E
polarization at resonance (70 MHz).
In Figure 10.7 the intercept of each curve with the
horizontal axis indicates the ambient conditions (temperature
and relative humidity) that will produce a rectal temperature
of 39.2ºC with no irradiation. For example, with a
relative humidity of 80% and an ambient temperature of
42ºC, the is zero--which means that under these
conditions a rectal temperature of 39.2ºC
will occur in 1 h with no irradiation. Similarly, the
curve shows that if the ambient temperature were 41ºC
and the relative humidity 80%, the would be 1.25
W/kg--under these conditions a rectal temperature of
39.2ºC would be reached in 60 min. The other curves in
the figure indicate that the same SAR (1.25 W/kg) would occur
at 49ºC and 50% relative humidity and at 63ºC and
20% relative humidity. From the ordinate on the right, we
read that at this , the incident power density for E
polarization at resonance would be 5 mW/cm². The
incident power densities at other frequencies and/or
polarizations can be determined by using the dosimetric
curves to find what power density produces an SAR of 1.25
W/kg for the given frequency and polarization in
question.
values in an average man,
unclothed and quiet, irradiated by an electromagnetic
planewave with E polarization at resonance (about 70 MHz).
Dashed horizontal lines indicate the psychrometric conditions
(in still air) that yield an of 1.25 W/kg and 0.4 W/kg
at this frequency.If the ambient temperature were 41ºC and the
relative humidity only 20%, a very high SAR would be required
to produce a rectal temperature of 39.2ºC in 60 min, a
value too high to be read from Figure 10.7. This shows that,
as expected, in warm environments the relative humidity has a
great effect on the body's ability to dissipate an added
thermal burden by evaporation. We strongly emphasize that the
is only an estimate of the upper limit of thermal
tolerance for a healthy nude man. Many other factors must be
considered, not the least of which is the great disparity in
thermoregulatory response from individual to individual.
Figure 10.7 shows the relative independence of the
on the prevailing ambient temperature at any given ambient
humidity level. Thus at such moderate SARs, hyperthermic
levels of body temperature can be expected only if the body
is already operating at near-critical environmental
conditions. Under such hostile conditions even small
increases in metabolic heat production, such as very light
work, will also initiate an increase in the body temperature.
The basis for RF exposure guidelines currently in force, 0.4
W/kg, is also indicated on the curves in Figure 10.7 under
the assumption of a 60-min average time. (The 6-min averaging
time specified in the current guidelines is far too short to
achieve a thermal steady state such as that represented in
Figure 10.7.) The reduction in ambient temperature required,
at any relative humidity, to accommodate an of 0.4
W/kg is less than can be precisely achieved or measured,
given present technology; therefore, no temperature or
humidity factors should be used to adjust 0.4-W/kg RF
exposures.
A healthy person exposed to the environments represented in the SAR curves would be expected to experience considerable thermal discomfort along with the rise in core temperature, rise in heart rate, and profuse sweating. All of these responses would increase over time until, at about 60 min, the person would be on the verge of collapse and exhibiting the unpleasant but reversible symptoms reported in experiments on human heat tolerance.
Because of the approximations used in the calculations described here and the great differences in thermoregulatory response found from person to person, we emphasize that the calculated data given in this handbook are intended to serve only as guidelines and to give a qualitative indication of anticipated responses.
Go to Chapter 11.
Return to Table of Contents.
Last modified: June 14, 1997