Range |
||||||
| A. One-dimensional models |
||||||
| Infinite plane tissue layers (isotropic) | Multilayers | Planewave | Transmission-line model | Unlimited | a | Good only at high frequencies where the body curvature can be neglected. Can predict y/4 type resonances but not body resonance. |
| Two layers | Rectangular aperature | Fourier transform technique and field matching on common boundaries | 433-2450 MHz | b, c | Used to calculate relative heating patterns. | |
| (Anisotropic) | Multilayers | Planewave | Transmission-line model (together with Thevenin's theorem) | 0.001-100 MHz | d | Used to calculate effects of tissue anisotropy (at low frequencies) on microwave fields and power absorption. Small effects observed at higher frequencies (above 10 MHz). |
| Semi-infinite homogeneous slab | One layer | Nonperiodic electric field with TE and TM components | Planewave spectrum analysis | All calculations at 2450 MHz |
e | Near-field analysis of aperture sources. |
| Six layers | E-polarized planewave | Optical refraction--Snell's law | Up to 3.0 GHz | f | Layering increases average SAR; an enhancement factor needed to correct results from homogeneous models. | |
| Homogeneous semi-infinite slab and multi-layered slab | --- | Near field of a source leaking radiation | Planewave-spectrum approach | 2450 MHz | g, h | For fields nearly constant over at least a free-space wavelength, energy deposition equal to or less than that resulting from planewave exposure. In the analysis, coupling of target to source not taken into account. |
| B. Two-dimensional models | ||||||
| Infinite circular cylinder | Length l= 1.75 m, radius a = 11.3 cm; l = 14 cm, a = 1.58 cm | Planewave | Mode-matching technique and geometrical optics |
300-6000 MHz | i, j | In good agreement with geometrical optics at the high-frequency limit. |
| Radius such that (formula) koa < 2.4 | Coaxial loop antenna | Long-wavelength approximation method | Depends on (formula) koa < 2.4 | k | Formulation simple to use, but valid results are in low-frequency range. Power absorption coefficient is plotted against loop dimensions and cylinder radius. | |
| 5- and 10- cm-radius cylinders in presence of a reflector | Planewave TE and TH with k vector normal to plane of a reflector | Point-matching method combined with imaging | Up to 1 GHz | l | SAR calculated as function of frequency and distance from reflector. | |
| Radius: 2.24-24 cm |
Planewave E and H polarization | a. Geometrical optics approximation b. Mode-matching technique |
200-100 GHz | j | At higher frequencies the two methods give same result. Average SAR results tally with those from prolate spheroidal models at higher frequencies. | |
| Multilayered infinite circular cylinder | --- | Planewave | Mode-matching technique and moment method | 433-2450 MHz | m, n | Microwave heating calculated in simulated human thigh. |
| Three layers | Direct con- tact aperture source (TE10 mode) |
Field expansion in terms of three-dimensional cylindrical waves and matching the boundary conditions | 433-2450 MHz | o | Microwave heating calculated in phantom models of human limbs exposed to a direct-contact aperture source. | |
| Multilayered cylinders of arbitrary cross section | a = 1.5 b, a = 0.239 m, b = 0.159 m for elliptical-cal cylinder | Planewave | Surface integral equations derived via vector Green's theorem and boundary condition | All calculations at 300 MHz | p | Calculations made for one-and two-layered circular and elliptical cylinders. |
| 17.5- x 19- cm triple-layered model | Planewave TM | Finite element | 433 MHz | q | Finite element method and variational calculus used to approximately calculate internal fields. Results presented only for normalized inside field. | |
| Multilayered infinite circular cylinders | Outer radius 11.28 cm | Planewave E and H polarization | 10 MHz-10 GHz | r | Absorption effects due to clothing are negligible below 2 GHz. Layering changes average SAR values in the 0.4- to 8-GHz frequency range. | |
| Homogeneous infinite cylinder | 62.6 x 62.6 cm | Planewave E polarization | Stacked two-dimensional spectral iterative technique (SIT) | 915 MHz, 2450 MHz | s | Method based on modeling the body by a set of planar parallel slabs and utilizing a convolution-type relationship between a current distribution on any slab and the field due to this current. Calculated data for the SAR distribution are given for two |
| Homogeneous infinite circular cylinder | radius = 5 cm | Near field of electric and magnetic line sources | Mode-matching technique | 27, 100, and 300 MHz | t | With proper choice of geometry and polariza-tion of the sources, it is possible to have deep penetration with maximum heating at the center and to move the maximum around. |
| Inhomogeneous infinite cylinders with arbitrary cross section | Cross section of a human torso | EM planewave and a sole-noidal field | Galerkin's method with linear basis function | Low-frequency region | u | Arbitrarily shaped polygonal cells are used to allow more accurate modeling of complex objects without excessive matrix sizes. |
| Annular phased array system | Moment method with pulse basis function | 70 MHz | v | SAR distribution calculated in two-dimensional models of cross sections of the human body. Numerical results agree with measured values in central region of the cross section. | ||
| C. Three-dimensional models |
||||||
| Finnite planar model | 16 x 12 x 4 cm for a fat muscle tissue block and 3 x 0.5 x 0.5 y for a muscle | Planewave | Tensor integral equation for the electric field inside the body | Results presented up to 2.45 GHz | w | Method applicable for heterogeneous biological bodies. |
| Finite circular cylinder | Height/radius l/ro = 12.68 | E-polarized planewave | a. Antenna theory b. Curve fitting used along with circuit theory |
1-60 MHz | x | For human model in direct contact with a ground plane, an order-of-magnitude enhancement tin SAR value may occur at frequencies below resonance. Enhancement rapidly decreases as model moves away from ground plane. Separation distance of about 7.5 cm from ground plane is sufficient to restore free-space absorption characteristics. |
| Spherical model | Radius of the sphere r = 10 cm | Planewave | Mie theory | 10-10,000 Mhz | y, z | Examined distribution of generated heat. |
| r = 25.57 cm | Planewave | Mie theory | 1-20 MHz | aa,bb | Power deposition in a spherical model of man--70 kg. | |
| r = 5 cm | Planewave | Mie theory | 10-12,000 MHz | cc | Distribution of heating potential. | |
| 4r = 10 cm | Planewave | Mie theory | 100-10,000 MHz | Type of nonuniformity described in a radius-frequency diagram. Localized heating for 8 cm < a < 0.1 cm in the frequency range 300 MHz < f < 12 GHz is described. | ||
| 2 < r < 50 cm experimental results for r = 3 and 7 cm |
Planewave | Mic theory | 915 and 2450 MHz | dd | Used to calculate heating patterns in mammalian brains. Selective absorption also indicated. | |
| Human head (7-cm radius) and infra-human | E-polarized planewave | Tensor integral equation method | 918 mHz for infrahuman head; 2450 MHz for human head | ee | Comparison made between heating of spherical and realistic models of humans and infrahuman heads. Lower EM heating induced in brain of realistic model than spherical model. Skull's bony structure tends to attenuate heating of the brain, including the eyes. | |
| Multilayered spherical model | Primate cranial structure of rhesus macaque monkey | Planewave | Mie theory | Most of the results, 3 GHz | ff | results given of average SAR and mean square electric field in equatorial plane |
| Human skull, r = 7-10 cm | Planewave | Mie theory | 0.1-3 GHz | gg | Additional SAR peak recognized at about 2.1 GHz. This is due to the y/r impedance matching effect which was also recognized in planar model (Schwan, 1968;;). | |
| Human and animal heads, r = 3.3-10 cm | Planewave | Mie theory | 0.1-10 GHz | hh | Energy distribution examined in three spheres--3.3-, 6-, and 10-cm radii--with emphasis on strong localized heating. | |
| Outer radius maximum value = 6.6 cm | Planewave | Mie theory | Results presented, 433 < f < 6000 MHz | ii | Examined SAR distribution in different layers. | |
| Six-layered cranial structure of maximum radius 3.3 cm | a. Current loop p | z b. Electric dipole m | z, both axially above the model |
State-space formulation | Rresults only at 3 GHz | jj, kk | Model allows for an idealized continuously inhomogeneous structure. Heat potential distributions are calculated | |
| Prolate spheroid /td> | a = 1 m and a/b = 7.73, volume = 0.07 m3 and a/b up to 10 | Planewave magnetic, electric, and cross polarization | Perturbation theory, based on expanding all fields in a power series of -jk | Up to 30 MHz | ll | Used to calculate the first-order internal electric field and SAR |
| 0.02 < a < 0.0875 m, 2 < a/b < 6.34 | Planewave magnetic, electric, and cross polarization | Perturbation analysis | Up to 30 MHz for man model; up to 1 GHz for mouse model | d | Average SAR presented as function of angle of incidence. | |
| 3 < a < 10 cm, a/b = 3.6 | Planewave cross polarization | Using the vector spheroidal wave function expansion | 100 and 2450 MHz | mm, nn | Results presented for 915 and 2450 MHz. In Lin and Wu (1977),, peak SAR was plotted for f = 10-3000 MHz for a = 3 cm and b = 2 cm. | |
| Up to man-size model a = 0.875, a/b = 6.34 | Planewave | Extended boundary condition method | At and slightly pastg resonance (-60 MHz for 2/3 muscle tissue of man-size model) | oo, pp | Good results up to resonance for average-man model. Frequency limited because of ill- conditioned matrix. For lower dielectric constants, the method can be used up to higher frequency limits. | |
| Man and animal sizes | Planewave | Geometrical optics | 20-100 GHz for man model, f > 80 GHz for rat model | i, qq | Based on dividing surface of prolate spheroid into small planar subareas, all power transmitted into the spheroid is assumed to be absorbed and secondary internal reflections are neglected. Lower frequency limit is based on convergence within 20% of Mie solution for sphere with a radius = b of the spheroid. | |
| a/b = 6.34, a = 0.875 m, weight = 70 kg | E-polarized planewave | Empirical curve-fittingprocedure | 10 Mhz-10GHz | rr | Provides simple empirical formula for calculating average SAR over broad-frequency band. Formula is only for E-polarized incident planewaves. | |
| Planewave E, H, and K polarization | Geometrical optics approximation | 6 GHz and beyond | ss | Method valid only in the frequency range where the body dimensions >> |
||
| 1.25 < a/b < 1.5, 0.297 < a < 0.335 m, volume = 0.07 m3 | Planewave E, H, and K polarization | Point-matching technique | Up to resonance of 130 MHz | tt | Absorbed power density plotted for spherical-like model. Solution does not converge for a/b > 1.5. | |
| a/b = 6.34, a = 0.875 m, volume = 0.7 m3 | Near field of electric dipole, E and K polarization | Extended boundary condition method | Results at 27 MHz | uu | For E polarization, average SAR oscillatges around its planewave value. For K polarization, SRA distribution suggests possible enhancement at regions of small radius of curvature. | |
| a/b = 6.34, a = 0.875 m, weight = 70 kg | Electric dipole located paralle to major axis of spheroid | Long-wavelength approximation method | Results at 27 MHz | vv | Analysis useful where long-wavelength approximation is valid but wave impedances are not 377 ?, and for near-field irradiation in which incident fields are quasi-uniform. | |
| Near field of a short electric dipole | Long-wavelength analysis | 27.12 MHz | ww | Average SARs in a prolate spheroidal model of man are essentially the same as those for a block model of man at 27.12 MHz, even in near fields. For purposes of average SAR, this allows use of the simpler and less expensive prolate spheroidal calculations. | ||
| Near fields of aperture sources | Extended boundary condition method | 27 MHz | xx, yy | Average SAR and the SAR distribution due to near fields of large and small aperture sources are given. Calculated results conform to the understanding previously obtained from studying irradiation of the spheroidal models by EM planewave and by n ear fields of various elementary radiation sources. | ||
| Spherically capped cylinder | The average man model and the small rat model | EM planewave | Surface integral equation | 80 MHz to 2.45 GHz | zz | Average SAR curves for E, H, and K polarizations intersect at a frequency just above resonance, about 800 MHz for man models. This may be useful in cases where the average SAR must be independent of animal position. |
| Prolate spheroid | · a/b = 6.34, a = 0.875 m, weight = 70 kg
· a/b = 3.1, a = 20 cm, weight = 3.5 kg · a/b = 3, a = 3.5 cm, weight = 20 g |
Small coaxial loop antenna | Extended boundary condition method | 10-600 MHz | ab | SAR distribution and average SAR are plotted as a function of separation distance from the loop. For distances less than 5  , average SAR values oscillate about the far-field value. , average SAR values oscillate about the far-field value. |
| Prolate spheroid | a/b = 6.34, a = 0.875 m, weight = 70 kg | Planewave E and K polarizations | Iterative extended boundary condition method | 27-300 MHz | ad, ae | An iterative procedure for improving stability and extending frequency range of the extended boundary condition method (EBCM). Calculated data for SAR distribution and average SARs in the resonance and postresonance frequency range are presented. |
| Axisymmetric cranial structure | height = 22.6 cm, volume = 4189 cm3 | EM planewave | Finite element method | 1 and 3 GHz | af | Model composed of upper concentric spheres and lower concentric spheroids. Curves for SAR distribution in brain region are presented for detached model of the human cranial structure. |
| Ellipsoidal model | Man model a = 0.875 m, volume = 0.07 m3, and b/c = 2 | Planewave | Pertgurbation technique | 1-30 MHz for man model | ag | First-order analysis valid for long-wave-length a/ < 0.1. Curves of SAR vs. frequency show SAR to be strong function of size and orientation of the ellipsoid in the incident field. Strongest absorption was found when electric-field vector of the incident planewave was along the longest dimension of the ellipsoid. < 0.1. Curves of SAR vs. frequency show SAR to be strong function of size and orientation of the ellipsoid in the incident field. Strongest absorption was found when electric-field vector of the incident planewave was along the longest dimension of the ellipsoid. |
| Man and animal model 0.05 < 2a < 1.8, 1.7 < a/b < 4.5, and 1.3 < b/c < 2 | Planewave | Perturbation technique | Up to 30 MHz for man model and to 1 GHz for the mouse | ah | Data used to extrapolate results of observed irradiation effects in animals to those expected to be observed in humans. | |
| Ellipsoid | Model of breast carcinoma embedded in nonabsorbing dielectric | Planewave | Boundary value solution in spheroidal coordinates | Results at 2450 MHz, 5.8 GHz, 10 GHz | ai | Three-dimensional and densitographic pictures of electromagnetic-field distribution with locations of hot spots shown. |
| Body-of-revolution model | Sphere resting on base of conical body; total height = 1.78 m | Vertically and horizontally polarized planewave | Surface integral equation method | Results at 30, 80, and 300 MHz | aj | Strongest power deposition is for field polarized along longest dimension and for frequencies near the first resonance (i.e., 80 MHz); hot spots predicted in neck region. |
| Block model of man | Height = 1.7 m, 120 cells; cell size was kept smaller than 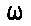 o/4 o/4 |
Planewave | Tensor integral equation method | Up to 500 MHz | ak, al | Integral equation solved by dividing the body into N cells, assuming a constant field inside each cell, and solving for the 3N unknowns using point matching. Also, hot spots are illustrated. |
| Height = 1.7 m, 180 cells; cell size < 10 cm | Planewave | Moment-method solution of electric-field integral equation | Up to 200 MHz | am | Chen and Guru's work (1977) extended by a. Using interpolant between field values at cell centers before carrying out the volume integral. b. Choosing cell sizes and locations for realistic model of man. |
|
| Block model | Height = 1.75 m, weight = 70 kg | E-polarized planewave | Image theory and moment method | Less than 100 MHz | an | Experimental data support numerical results. Resonant frequency shifts from 77 MHz in free space to 47 MHz when standing on a ground plane. An order-of-magnitude enhancement in SAR values is predicted at frequencies below 30 MHz. |
| Moment method | 10-600 MHz | am | Numerical calculations of absorbed energy deposition made for human model constructed with careful attention to both biometric and anatomical diagrams. | |||
| Planewave, vertical, and horizontal polarization | Tensor integral equation method | Up to 500 MHz | ao | Results for average SAR are compared with existing experimental results. Resonance and the effect of body heterogeneity on the induced field are studied. | ||
| Inhomogeneous block model of man | Height=- 1.75 m, weight = 70 kg | Planewave | Moment method with pulse basis function | 27.12 MHz and 77 MHz | ap | Whole-body and part-body average SAR for man in free space and under grounded conditions are given as function of angle of incident. In general for frequencies considered, average SAR varies smoothly with angle between the extrema. |
| Block model of man | Height = 1.75 m, weight = 70 kg | Near-field exposure | An empirical relationship | Less than 350 MHz | aq | Empirical formula for average SAR in man under a two-dimensional near-field exposure. Average SAR is lower for n ear-field exposure than for planewave irradiation conditions. |
| Block model and cylinddrical model of man | Height = 1.75 m, weight = 70 kg | Near field of resonant thin-wire antenna | Moment method and finite element method | 45 MHz, 80 MHz, and 200 MHz | ar, as | Temperature distribution in cylindrical model of man is calculated by a finite element solution of the transient heat conduction equation in which the internal heat generation is due to metabolism and absorption of EM energy. At least 50 W incident power is required before the body experiences any significant thermal effect from the near-zone antenna fields. |
| Block model | Height = 1.68 m, max diameter = 0.36 m; height = 2.22 cm, max diameter = 3.8 m | Uniform RF magnetic field | Solution of vector potential by moment method | 10-750 MHz | at | Electric fields induced by RF magnetic field inside a sphere, finite circular cylinder, and phantom models of humans are calculated. Calculated data are verified by experimental values and existing theoretical results. |
| Height = 1.7 m, weight = 68 kg | Near field of a dipole antenna | Moment method with pulse basis function | 27, 80, and 90 MHz | au | Average SAR in the body as a function of antenna-body spacing is calculated at 27 MHz. Calculated SAR-distribution data agree qualitatively with the experiment values. | |
| Inhomogeneous block model | Height = 1.75 m, weight = 70 kg | Near field of an RF sealer | Moment method with pulse basis function | Less than 350 MHz | av | Planewave spectrum approach used to calculate average SAR and SAR distribution in an inhomogeneous block model of man for a prescribed two-dimensional leakage electric field. Average SAR under near-field conditions is always less than or equal to the far-field planewave value. |
| Inhomogeneous block model of man | Height = 1.75 m, weight = 70 kg | Planewave E polarization | Moment method with pulse basis functions | 27.12 MHz | aw | Average SAR and SAR distributions are obtained for man models with 180-1132 cells by the moment method with pulse basis function. Calculated values of average SAR increase with the number of cells used. |
REFERENCES:
| a. Schwan, 1968 | aa. Johnson and Guy, 1972 | ab. Lakhtakia et al., 1982b |
| b. Guy, 1971b | bb. Lin et al., 1973b | ac. Lakhtakia et al., 1981 |
| c. Guy and Lehmann, 1966 | cc. Kritikos and Schwan, 1975 | ad. Iskander et al., 1983 |
| d. Johnson et al., 1975 | dd. Lin et al., 1973a | ae. Iskander et al., 1982b |
| e. Chatterjee, 1979 | ee. Rukspollmuang and Chen, 1979 | af. Morgan, 1981 |
| f. Barber et al., 1979 | ff. Shapiro et al., 1971 | ag. Massoudi et al., 1977a |
| g. Chatterjee et al., 1980a | gg. Joines and Spiegel, 1974 | ah. Massoudi et al., 1977b |
| h. Chatterjee et al., 1980b | hh. Weil, 1975 | ai. Zimmer and Gros, 1979 |
| i. Durney et al., 1976 | ii. Neuder et al., 1976 | aj. Wu, 1979 |
| j. Massoudi et al, 1979a | jj. Hizal and Tosun, 1973 | ak. Chen and Guru, 1977b |
| k. Yoneyama et al., 1979 | kk. Hizal and Baykal, 1978 | al. Chen et al., 1976 |
| l. Ruppin, 1979 | ll. Durney et al., 1975 | am. Hagmann et al., 1979a |
| m. Ho, 1975a | mm. Lin and Wu, 1977 | an. Hagmann and Gandhi, 1979 |
| n. Ho et al., 1969 | nn. Wu and Lin, 1977 | ao. Chen and Guru, 1977c |
| o. Ho et al., 1971 | oo. Barber, 1977a | ap. Hagmann et al., 1981 |
| p. Wu and Tsai, 1977 | pp. Barber, 1977b | aq. Chatterjee et al., 1982a |
| q. Neuder and Meijer, 1076 | qq. Rowlandson and Barber, 1977 | ar. Spiegel, 1982 |
| r. Massoudi et al., 1979b | rr. Durney et al., 1979 | as. Spiegel et al., 1980 |
| s. Kastner and Mittra, 1983 | ss. Rowlandson and Barber, 1979 | at. Lee and Chen, 1982 |
| t. Morita and Andersen, 1982 | tt. Ruppin, 1978 | au. Karimullah et al., 1980 |
| u. Hill et al., 1983 | uu. Iskander et al., 1980 | av. Chatterjee et al., 1980c |
| v. Iskander et al., 1982a | vv. Massoudi et al., 1980 | aq. Deford et al., 1983 |